Morphologie cristalline
Sommaire : Morphologie cristalline
Notions générales
Un corps amorphe se caractérise par l’absence de tout arrangement intérieur et, de ce fait, n’a ni forme définie, ni direction. Il est limité par des surfaces irrégulières.
À l’inverse, dans un minéral cristallisé, les atomes se disposent régulièrement. Un tel minéral possède des directions privilégiées qui lui donnent des propriétés bien définies. Il se présente sous forme polyédrique susceptible de définition géométrique. On l’appelle un cristal.
Bien qu’un même cristal puisse se présenter sous différentes combinaisons de formes cristallines variées, ces dernières se rattachent toujours à une forme régulière car on peut considérer qu’au cours de sa croissance, les faces se sont déplacées parallèlement à elles-mêmes. L’étude des angles qu’elles forment entre elles a conduit à formuler une loi physique dite de la constance de l’angle dièdre (Se dit d’un angle qui est formé par la rencontre de deux surfaces ou de deux plans qui se coupent), à savoir que 73 chez des cristaux de la même espèce, les angles dièdres formés par les faces homologues sont égaux dans des conditions de température et de pression identiques.
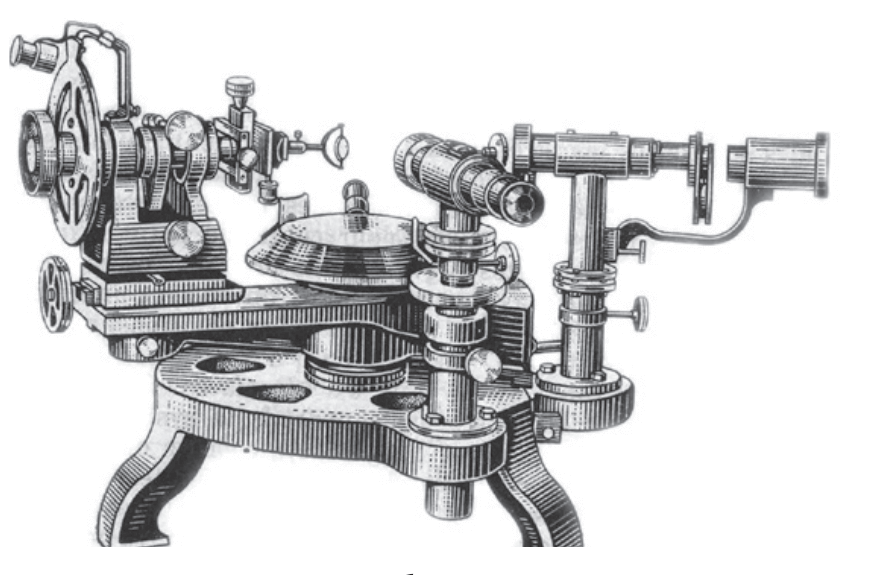
La mesure des angles se fait à l’aide d’appareils appelés goniomètres dont il existe plusieurs types. Le plus ancien est le goniomètre d’application. On l’utilise surtout avec les cristaux de grande taille. Pour les petits cristaux, ou chaque fois que l’on désire une mesure très précise, on lui préfère le goniomètre à réflexion qui permet, en outre, la mesure de l’indice de réfraction. L’instrument le plus récent est le goniomètre à cellule photoélectrique qui autorise des mesures extrêmement précises et qui enregistre les données relatives à la morphologie des cristaux. La plupart des minéraux sont des cristaux dont la forme externe ne reflète pas la régularité de la structure interne.
Pour permettre l’étude et la classification des cristaux, la cristallographie les a divisé suivant leur symétrie tout en ramenant la structure de chacun d’eux à une maille élémentaire, ou cellule unitaire imaginaire, schématisant le plus petit arrangement cristallin d’un minéral considéré.
Les éléments de symétrie d’un cristal sont :
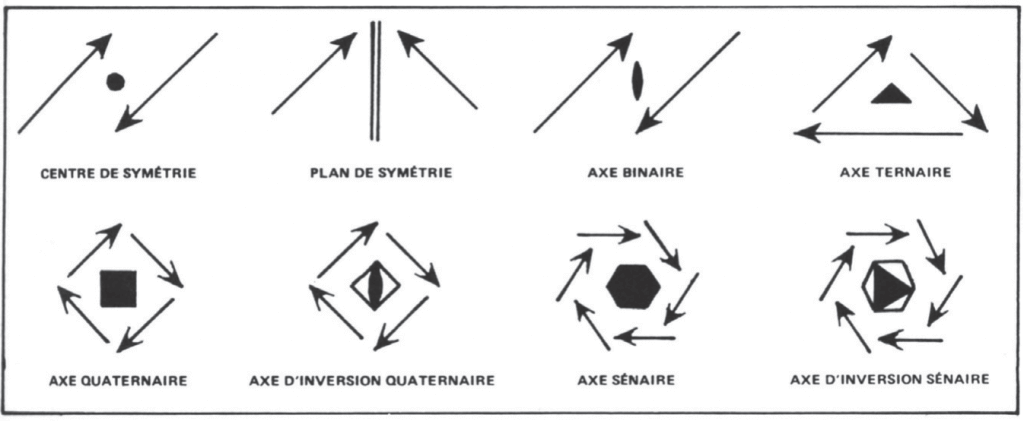
- Le centre de symétrie (à ne pas confondre avec le centre de gravité) qui caractérise tout cristal dont les faces sont parallèles deux à deux, comme dans le cube. Certains solides, tel le tétraèdre, n’ont pas de centre de symétrie ;
- Le plan de symétrie qui, à la manière d’un miroir, partage un cristal en deux parties opposées identiques;
- Les axes de symétrie ou de rotation, autour desquels un cristal peut pivoter et occuper un nombre défini de positions le retrouvant identique à lui-même. Ainsi, un dé lancé sur une table présentera toujours une face semblable à celle qui reposait sur la table, quel que soit le nombre de rotations qu’il aura effectuées autour de ses axes. Les angles caractéristiques sont 180°, 120°, 90° ou 60°.
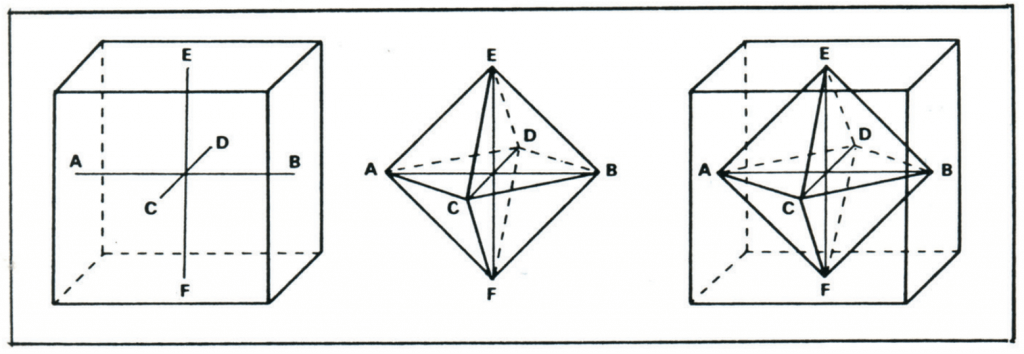
Un cristal peut posséder plusieurs axes de symétrie et chaque axe peut permettre au même cristal d’occuper plusieurs positions le retrouvant identique à lui-même. Selon le nombre de ces positions, on dit qu’il s’agit d’un axe d’ordre 2, 3, 4, 6. Ainsi, le cube a trois axes d’ordre 4, quatre axes d’ordre 3 et six axes d’ordre 2, ce qui s’abrège en 3A4, 4A3, 6A2.
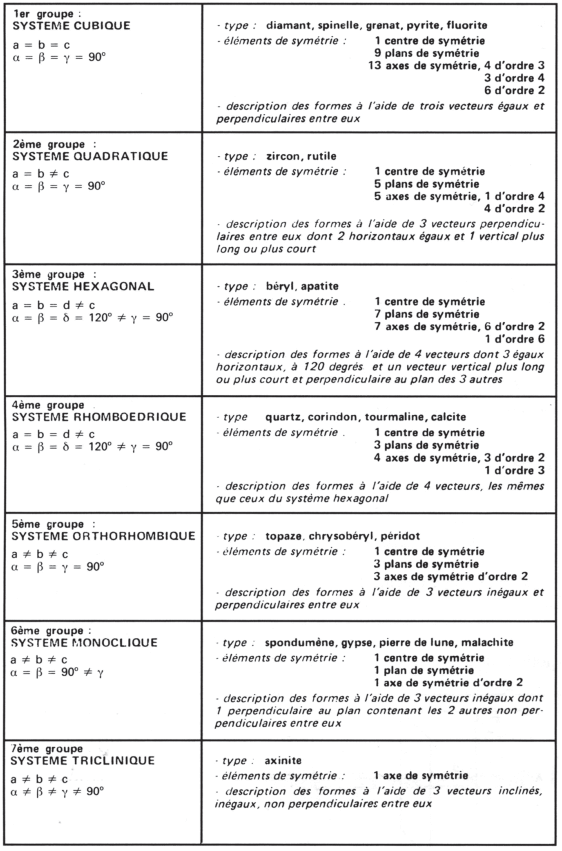
En fonction de ces éléments de symétrie, les cristaux ont été classés en 32 classes distinctes de systèmes symétriques, rangées en 7 systèmes de groupes cristallins (voir tableau).
Chacun de ces systèmes est ramené à la cellule unitaire cristalline en lui associant les notions de longueurs et d’angles cristallographiques.
Les axes de symétrie des diamants ne sont pas la même chose que le critère de qualité portant le nom de symétrie. Découvrez tout ce qu’il faut savoir sur le critère de symétrie dans les diamants taillés
Morphologie cristalline du diamant
Formes générales
Le diamant cristallise dans le système cubique et ses formes cristallines sont nombreuses. Les formes simples sont :
- le cube présentant 6 faces, 12 arêtes, 8 sommets;
- l’octaèdre présentant 8 faces triangulaires, 12 arêtes, 6 sommets;
- le rhombododécaèdre présentant 12 faces en losange, 24 arêtes, 14 sommets;
- le tétrahexaèdre présentant 24 faces;
- le trapézoèdre présentant 24 faces;
- le trisoctaèdre présentant 24 faces triangulaires;
- l’hexoctaèdre présentant 48 faces.

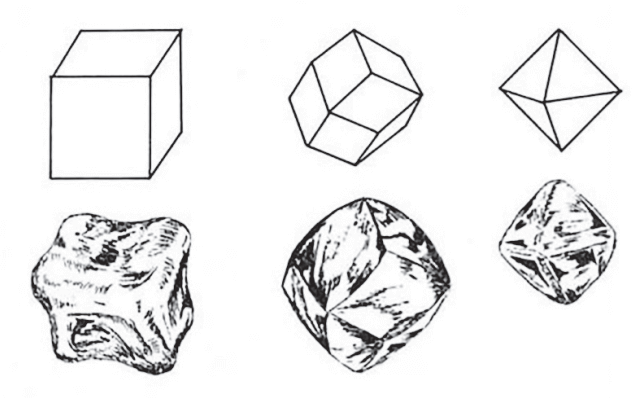
Ces différentes formes sont dérivées de la structure de base du cube à la suite de la troncature des arêtes ou des sommets.
Le diamant se présente sous trois formes cristallines principales dont la plus fréquente est celle de l’octaèdre, suivie de celle du dodécaèdre, puis de celle du cube, ou bien d’une combinaison entre elles. Bien que différentes, ces trois formes ont exactement la même structure interne et offrent, en conséquence, les mêmes possibilités de taille. On a donc :
- L’octaèdre qui est la forme dérivée du tétraèdre ou du cube tronquant chacun de ses sommets. Certains octaèdres ont des faces lisses et planes comme celles d’un miroir et possèdent, parfois, à leur surface, de petites figures particulières appelées « trigons » en creux. Ce sont 80 de petites marques cristallines externes, parfois visibles à l’œil nu, en forme de triangle équilatéral, strictement alignées et dirigées dans le même sens. Leur base est le plus souvent orientée vers le sommet de la face de l’octaèdre sur laquelle elles se trouvent. La forme parfaite de l’octaèdre serait le résultat d’une croissance lente. Dans le cas où cette croissance a été perturbée, l’octaèdre présente des faces en lamelles empilées et est souvent arrondi par dissolution ; il présente parfois des arêtes concaves comme des gouttières;
- Le rhombododécaèdre qui présente des arêtes et des faces courbes losangiques soit, en somme, les 6 pointes de l’octaèdre plus 8 pointes surélevées résultant de la dissolution trisoctaèdre ;
- Le cube : il est habituellement grêlé et mat, rarement transparent et ses faces sont souvent concaves;
- D’autres formes cristallines moins fréquentes peuvent se rencontrer, comme le trisoctaèdre qui a une pyramide arrondie sur chaque face octaédrique ou bien l’hexoctaèdre qui est très rare et qu’on trouve principalement en Inde.
Il existe aussi des formes cristallines inhabituelles dont une partie de la pierre est un octaèdre et l’autre partie, un dodécaèdre.

Formes maclées
Une macle est l’association régulière de deux ou plusieurs cristaux d’orientations différentes, suivant des lois géométriques bien définies (lois de macle), directement liées à la symétrie du réseau du diamant. Ainsi il arrive que lors de leur formation, deux ou plusieurs cristaux distincts se trouvent réunis par une surface de cristallisation commune et se trouvent accolés les uns aux autres ou s’interpénètrent. Ces cristaux peuvent ne pas être de même grosseur, ou bien encore être réunis sous des orientations différentes. Dans le cas de macles par hémitropie, les deux cristaux sont réunis sur un même plan parallèle à deux faces opposées de l’octaèdre, l’orientation des deux individus cristallins se trouvant disposée, l’un par rapport à l’autre, à 180°.
Les pierres maclées se caractérisent souvent par des angles rentrants.
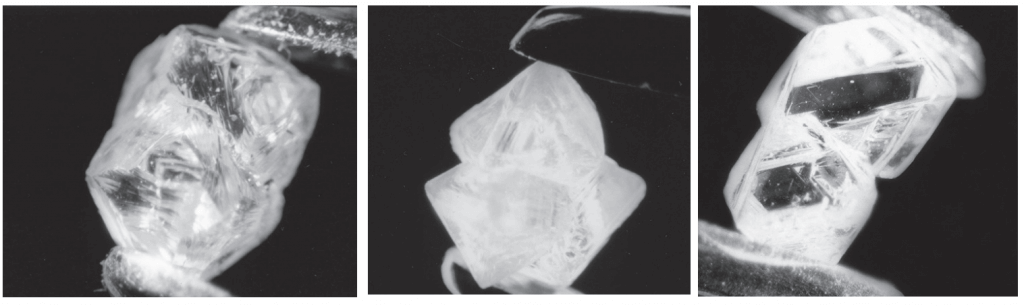
Autres formes
Certaines variétés souvent polycristallines de diamant ne sont pas utilisées en joaillerie. Elles ne sont cependant pas dénuées de toute valeur et trouvent leur emploi dans d’autres domaines comme celui de l’industrie. On peut citer parmi ces formes:
- Le bort ou boart, de cristallisation confuse, aux formes arrondies, sans clivage net principalement de couleur noire ou grise (densité : environ 3,50);
- Le shot bort, de forme sphérique ou ballas, à structure radiée et de qualité tenace (densité : environ 3,49);
- Le carbonado, très courant, se présentant sous forme d’un agglomérat de petits cristaux noirs ou gris, à reflets métalliques, légèrement poreux, ressemblant à du ciment ou à de la cendre (densité : environ 3,15);
- La framésite qui est un bort noir.
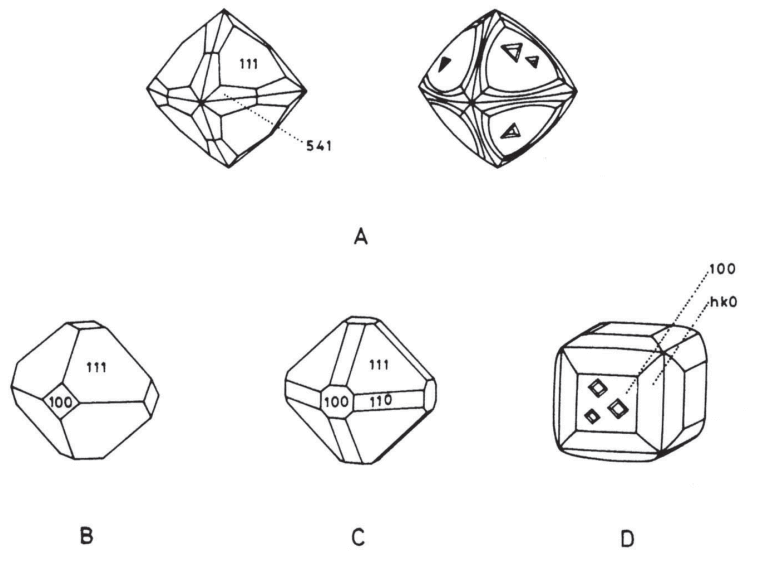
Indices de Miller
Miller appliqua à la cristallographie les méthodes de la géométrie analytique et créa un système de notation rationnelle pour désigner les faces au moyen d’indices.
© Dureté 10 – Eddy Vleeschdrager




